深層学習の説明性
- 0. 概要
- 1. 判断根拠の可視化
- 2. モデルの近似
- キーワードまとめ
Contents
0.章の概要
この章では、深層学習の説明性について解説しています。XAI(eXplainable AI)の概要から、CAM(Class Activation Map)、Grad-CAMなどの手法を用いて、モデルがどの特徴に注目したのかを可視化し、人間がその予測結果を直感的に理解できる方法について学んでいきます。また、SHAP(SHapley Additive exPlanations)などのモデル近似手法を用いて、各特徴の寄与度を計算し、モデル全体の予測にどの程度貢献したかを計算する手法についても説明していきます。
1. 判断根拠の可視化
学習キーワード: XAI (eXplainable AI)、CAM (Class Activation Map)、Grad-CAM
概要
XAI(eXplainable AI)とは、人間が機械学習モデルの予測結果を理解しやすくするために使われる手法です。 AIを利用する上で、モデルの予測結果に対して「どの部分が重要だったのか」を理解することはとても重要です。 ここでは、CAM(Class Activation Map)やGrad-CAM(Gradient-weighted Class Activation Map)などの手法を用いて、 モデルが「どの特徴に注目したのか」を可視化し、人間がその予測結果を直感的に理解できる方法について学んでいきます。
CAM(Class Activation Map)

出典: Zhou, B., Khosla, A., Lapedriza, A., Oliva, A., & Torralba, A. (2016). Learning Deep Features for Discriminative Localization.
arXiv preprint arXiv:1512.04150.
https://arxiv.org/abs/1512.04150 本図は教育目的で引用しています。
CAMの概要
CAM(Class Activation Map)は、主に画像認識置けるXAIの1つで、深層学習モデルがどの領域に注目しているのかを示す手法です。クラス分類に寄与した入力領域をHeatmapとして表示させることで、モデルの判断根拠を明確に理解することができます。
CAMを適用するためには、モデルの最終畳み込み層(Conv Layer)の出力と、グローバルアベレージプーリング(GAP)層を使用する必要があります。
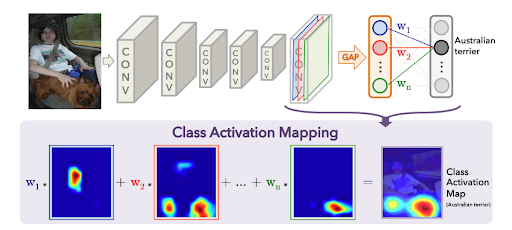
CAMの仕組み
出典: Zhou, B., Khosla, A., Lapedriza, A., Oliva, A., & Torralba, A. (2016). Learning Deep Features for Discriminative Localization.
arXiv preprint arXiv:1512.04150.
https://arxiv.org/abs/1512.04150 本図は教育目的で引用しています。
- まず、入力データをモデルに流し込み、最終畳み込み層(Conv Layer)の特徴マップを取得します。
- 次に、特徴マップにグローバルアベレージプーリング(GAP)を適用し、特徴マップの各チャネルの平均値を計算します。
- クラスごとの重み \( w_k^c \) を計算し、特徴マップの各チャネルに重みを乗算します。
- 重み付き特徴マップを合算し、クラスアクティベーションマップ(CAM) \( M_c \) を生成します。
- 最後に、CAM \( M_c \) を双線形補間やトランスポーズ畳み込みを用いて元画像と同じサイズに拡大する。
CAMの数式
仕組み手順を数式で表すと以下のようになります。
- \( S_c \):クラス \( c \) のSoftmaxスコア
- \( w_k^c \):クラス \( c \) に接続する重み
- \( f_k(x, y) \):\( k \) 番目の特徴マップの \( x, y \) 座標ピクセル
また、各ピクセルごとにクラス \( c \) である重要度を表すと、以下のようになります。(単純に上式を切り抜いただけ)
この式でクラス \( c \) の特徴マップの \( x, y \) 座標に関しての重要度を示すヒートマップが計算できます。
CAMの課題
CAMは、グローバルアベレージプーリング(GAP)層を使用したモデル(ResNetなど)でしか使えません。また、双線形補間やトランスポーズ畳み込みでCAMを拡大していますが、解像度が低いことが課題として残っています。一方、次に説明するGrad-CAMはモデル構造に依存せず、解像度の高い可視化を実現しました。
Grad-CAM(Gradient-weighted Class Activation Map)
Grad-CAMの概要
Grad-CAMは、畳み込み最終層の出力値に対する勾配を利用して、深層学習モデルが予測時に注目した領域を可視化する手法です。 CAMの拡張版であり、順伝播におけるGAP層を必要とせず、多様な構造のCNNに適用することができます。

出典: Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R., Parikh, D., & Batra, D. (2017). Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization.
arXiv preprint arXiv:1610.02391.
https://arxiv.org/abs/1610.02391 本図は教育目的で引用しています。
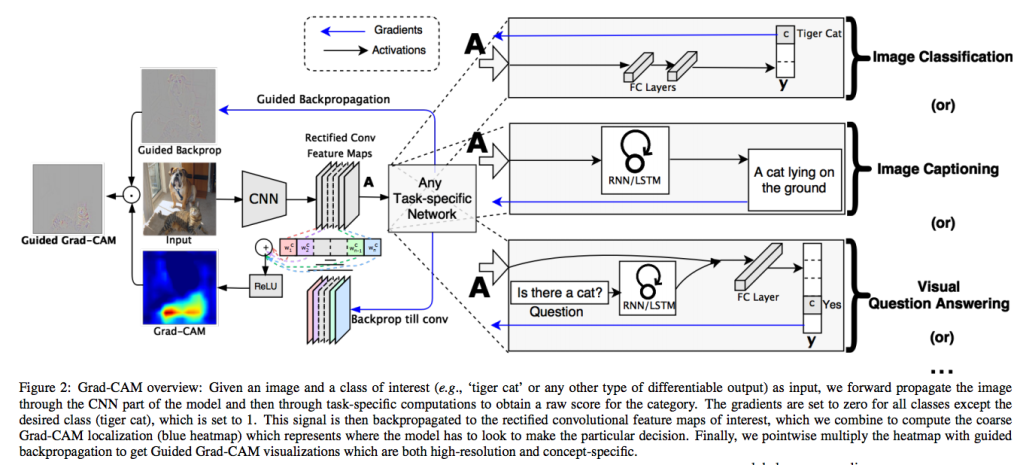
Grad-CAMの仕組み
出典: Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R., Parikh, D., & Batra, D. (2017). Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization.
arXiv preprint arXiv:1610.02391.
https://arxiv.org/abs/1610.02391 本図は教育目的で引用しています。
- 画像を順方向に入力し、畳み込み層と対象クラス \( y^c \) の分類スコア(ソフトマックスを行う前の値)を取得します。
- 分類結果を使って誤差逆伝搬し、対象クラス \( y^c \) に対する最終畳み込み層の特徴マップ \( A^k \) の勾配を計算します。
- 畳み込み層の勾配のグローバルアベレージプーリング(GAP)を取り、重み \( \alpha_k^c \) を取得します。
- \( \alpha_k^c \) を重みとした畳み込み層 \( A^k \) の重み付き和を取り、元の画像サイズにリサイズします。
- 最後に、不要な負の値を取り除くため、ReLU関数を適用します。
Grad-CAMの数式
仕組み手順を数式で表すと以下のようになります。
- \( L^c_{\text{Grad-CAM}} \):クラス \( c \) に対応するGrad-CAM。特徴マップの重みを合算した結果。
- \( \alpha_k^c \):特徴マップ \( k \) に対する重み。対象クラスにおけるその特徴マップの貢献度を表す。
- \( Z \):特徴マップの全ピクセル数。特徴マップの大きさを示す。
- \( A^k_{(i, j)} \):最終畳み込み層の特徴マップの座標 \((i,j)\)における値。
- \( y^c \):クラス \( c \) の出力値(ソフトマックスを行う前の値)。
上記の数式により、対象クラス \( y^c \) に対する重要領域を示すマップが得られます。 勾配自体を重みとして利用することで、GAP層が不要になり、モデル構造の柔軟性が向上しました。 また、 ReLU関数を適用することで、負の値(ノイズ)を除去することで、注目領域が直感的に解釈しやすくなります。
Guided Backpropagation
Guided Backpropagationは、特定のクラスの特徴を強調するために使用される手法で、順方向と逆方向の計算においてReLUフィルタを導入します。 順方向では負の値をゼロに設定し、逆方向では負の勾配を遮断します。 この仕組みにより、視覚化結果からノイズを除去し、直感的に理解しやすい結果を得られるようになりました。
Grad-CAMと併用することで、クラス分類に重要なピクセルを高解像度で視覚化することが可能になります。(Guided BackpropagationとGrad-CAMのアダマール積をとったものがGuided Grad-CAMと呼ばれます。仕組み図を参照ください。)
以下に論文より引用したGuided Backpropagationの解説図を示します。
出典: Springenberg, J. T., Dosovitskiy, A., Brox, T., & Riedmiller, M. (2015). Striving for Simplicity: The All Convolutional Net.
arXiv preprint arXiv:1412.6806.
https://arxiv.org/abs/1412.6806 本図は教育目的で引用しています。
2. モデルの近似
学習キーワード: 局所的な解釈、大域的な解釈、LIME、SHAP、Shapley Value、協力ゲーム理論
概要
ここでは、深層学習モデルが予測を行う仕組みを人間が理解できる形で表現する手法を解説します(モデルの近似)。 モデルの近似は大きく分けて、局所的な解釈と大域的な解釈に分類されます。
- 局所的な解釈:特定の入力に対するブラックボックスモデルの予測の根拠を提示することで説明とする方法を指します。LIMEが代表的な手法です。
- 大域的な解釈:複雑なブラックボックスモデルを可読性の高い解釈可能なモデルで表現することで説明とする方法を指します。SHAPが代表的な手法です。
LIME(Local Interpretable Model-agnostic Explanations)
LIMEは、局所的な解釈を提供するモデル説明手法で、特定のモデルの予測に対し、簡易な線形モデルを用いてその予測の根拠を可視化する技術で、様々な機械学習モデルに適応可能です。
LIMEの仕組み
LIMEの仕組みを簡単に説明すると、入力画像をパーツで切り分け、それを学習済みモデルに入力し、その予測結果を得ます。その後、入力画像(パーツ)と予測結果のペアを別の可読性の高いモデル学習する、といった流れになります。
具体的な手順は以下の通りです。
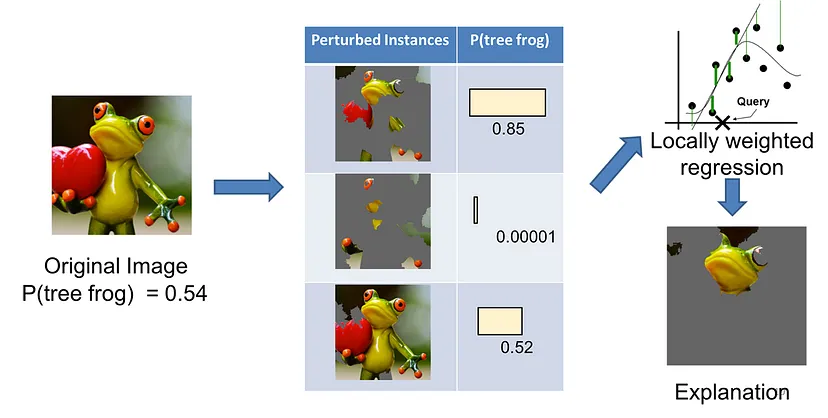
出典: https://towardsdatascience.com/understanding-how-lime-explains-predictions-d404e5d1829c
本図は教育目的で引用しています。
-
対象データの選定: 解釈したいモデルの予測結果と、それに対応する特定の入力データを選びます。(LIMEへの入力は1つの予測結果)
例: あるカエルの画像を1枚入力し、「カエル」と分類した理由を知りたい。 -
擬似データの生成: 入力データの周辺に類似するデータを生成します。
例: 画像なら一部のパーツを切り抜いたりし、テキストなら一部の単語を削除して新しいサンプルを作成します。 - モデルの予測結果を取得: 擬似データをモデルに入力し、それぞれの予測結果を取得します。
-
特徴の重み付け: 擬似データと元のデータの類似度を計算します。
例: ユークリッド距離やコサイン類似度を使い、元のデータに近い擬似データほど重要度を高く設定します。 - 線形モデルの学習: 擬似データを使用してローカルな線形モデルを学習し、特徴ごとに重みを算出します。
- 結果の可視化: 学習した線形モデルの結果を可視化し、予測に寄与した特徴をヒートマップやグラフとして表示します。
下図は、論文より引用したものですが、LIMEのイメージがわかりやすいと思います。赤い+が元々の分類器モデルでpositiveと判定された例、青い丸がnegativeの例です。強調された赤い+が解釈したい予測結果にあたり、この周辺にあるのが入力データからサンプリングした類似データについて予測した結果となります。それらを分断している黒い点線が、新しい解釈性の高い分類器です。
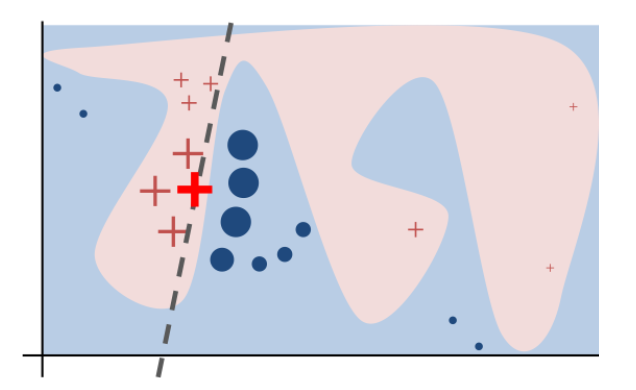
出典: Ribeiro, M. T., Singh, S., & Guestrin, C. (2016). “Why Should I Trust You?” Explaining the Predictions of Any Classifier.
arXiv preprint arXiv:1602.04938.
https://arxiv.org/abs/1602.04938 本図は教育目的で引用しています。
LIMEの数式
LIMEで押さえておくべき数式(損失関数)は、以下の通りです。
- \( \xi(x) \): 分類器 (\( g \)) を求めるための目的関数
- \( x \): 元の入力データ。
- \( G \): 解釈可能なモデルの集合。
- \( f \): 説明したい分類器
- \( g \): 線形モデル(LIMEが学習するローカル線形モデル)で、\( g \in G \)。
- \( \pi_x(z) \): 元の入力 \( x \) の類似度(近接度)。
- \( \Omega(g) \): 線形モデル \( g \) の複雑さを抑える正則化項。
- \( \mathcal{L}(f, g, \pi_x) \): 損失関数。
- \( z' \): 擬似データ。
- \( Z \): 擬似データの集合。
- \( D(x, z) \): 元の入力 \( x \) と擬似データ \( z \) の距離。
- \( \sigma \): 類似度の計算に使われるパラメータ。
\( D(x, z) \) が大きいほど、近接度は0に近づきます。つまり、元の入力と疑似データの入力が遠い場合は、説明したい分類器と線形モデル(LIMEが学習するローカル線形モデル)の差 \( (f(z) - g(z'))^2\)の差の影響は考えなくてよい(損失にならない)ということになります。
※最後に注意点として、LIMEはあくまでも局所的な解釈を提供するものであり、モデル全体の挙動を説明するものではありません。
SHAP(SHapley Additive exPlanations)
SHAP(SHapley Additive exPlanations)は、Shapley Valueという協力ゲーム理論から派生した概念を使用して、特徴の重要度を計算し、各特徴量の増減が、どれだけ予測に影響を与えるかを可視化する手法です。
各プレイヤーの貢献度に応じて、報酬をどう分配するかの概念を、機械学習に応用したものになります。また、SHAPは様々な機械学習モデルに適応可能です。
SHAPの仕組み
-
対象モデルと入力データの選定:
解釈したいモデルと特定の入力データ(例: 分類対象の画像やテキスト)を選びます。
例: 猫の画像を入力し、「猫」と分類された理由を解釈したい。 -
特徴の摂動とデータ生成:
選択した入力データに対し、各特徴をマスク(削除や置換)して擬似データを生成します。
例: 画像では一部のピクセルを黒く塗りつぶす、テキストでは特定の単語を削除する、など。 -
モデルの予測結果の取得:
擬似データをモデルに入力し、それぞれの予測結果(出力値)を取得します。
例: ピクセルをマスクした画像に対して「猫」と判断される確率の変化を記録します。 -
特徴の組み合わせに基づく影響度の計算:
特徴の有無(使用する/しない)によるモデルの出力変化を測定し、各特徴の影響度を計算します。
例: 猫の耳部分のピクセルがマスクされると「猫」と判断される確率が大幅に低下します。(←耳が重要な特徴量である可能性!) - ShapleyValueを基に寄与度を計算: 各特徴がモデル全体にどの程度寄与しているかを計算します。特徴間の相互作用を考慮し、公平に寄与度を分配します。
-
結果の可視化:
計算したSHAP値を用いて、各特徴の寄与度をヒートマップや棒グラフで視覚化します。
例: 猫画像を猫と分類した場合、猫の耳の領域がヒートマップで強調されたりします。
SHAPの数式
ゲーム理論における 特徴 \(i\) のShapleyValueの計算式は以下の通りです:
- \( \phi_i \) : 特徴 \(i\) のShapleyValue
- \( v(S) \) : 特徴の部分集合(S)を使ったときのゲームの価値
- \( N \) : 特徴の総数
- \( S \) : 特徴 \( i \) を除いた任意の部分集合(\( S \subseteq N \setminus \{i\} \))
- \( |S| \) : 部分集合 \( S \) の特徴の数
近似モデルの制約
複雑な学習済みモデルを簡単なモデルで近似する際には以下の3つの制約があります。重要ですので用語だけでも抑えましょう。
- Local accuracy:学習済みモデルと簡単なモデルの局所的な精度が等しくなるようにする。
- Missingness:モデルの予測に使用されなかった特徴量の寄与値は0。
- Consistency:異なるモデル間において、ある特徴量を除いた際の影響の大小と、寄与値の大小の関係性に一貫性がある。
SHAPをイメージするための計算例
Shapley Valueは、各特徴がモデル全体の予測にどれだけ貢献したかを公平に計算します。
以下の例では、3人のプレイヤー \( A, B, C \) が全員協力した場合に300点を取得しました。この300点はどの割合で分配するのが望ましいでしょうか?という問題定義で計算しています。
ゲームの状況- 3人で協力した際の総得点: 300点
- 利得関数: チーム \( S \) による得点は以下の表に示されています。
| チーム \( S \) ({}内のメンバーで取得した点数) | 得点 \( v(S) \) |
|---|---|
| 空集合 \( \{\} \) | 0 |
| \( \{A\} \) | 100 |
| \( \{B\} \) | 80 |
| \( \{C\} \) | 60 |
| \( \{A, B\} \) | 220 |
| \( \{A, C\} \) | 180 |
| \( \{B, C\} \) | 140 |
| \( \{A, B, C\} \) | 300 |
上の表を基に3人のShapley Valueを求めていきます。
復習:Shapley Valueの計算式ここで今回の目的に追わせて数式を解釈すると以下のようになります:
- \( S \): チームの部分集合(プレイヤー \( i \) を含まない)
- \( v(S) \): チーム \( S \) の得点
- \( |S| \): 部分集合 \( S \) のメンバー数
- \( N \): 全プレイヤーの集合(ここでは \( \{A, B, C\} \))
- 寄与度: \( v(S \cup \{A\}) - v(S) \)
- 重み: \( \frac{|S|!(|N| - |S| - 1)!}{|N|!} \)
| 部分集合 \( S \) | \( v(S) \) | \( v(S \cup \{A\}) \) | 寄与度: | 重み | 寄与度 × 重み |
|---|---|---|---|---|---|
| \( \{\} \) | 0 | 100 | 100 | \( \frac{1}{3} \) | 33.33 |
| \( \{B\} \) | 80 | 220 | 140 | \( \frac{1}{6} \) | 23.33 |
| \( \{C\} \) | 60 | 180 | 120 | \( \frac{1}{6} \) | 20.00 |
| \( \{B, C\} \) | 140 | 300 | 160 | \( \frac{1}{3} \) | 53.33 |
\( 33.33 + 23.33 + 20.00 + 53.33 = 130.00 \)
プレイヤー \( B \) に関する計算- 寄与度: \( v(S \cup \{A\}) - v(S) \)
- 重み: \( \frac{|S|!(|N| - |S| - 1)!}{|N|!} \)
| 部分集合 \( S \) | \( v(S) \) | \( v(S \cup \{B\}) \) | 寄与度 | 重み | 寄与度 × 重み |
|---|---|---|---|---|---|
| \( \{\} \) | 0 | 80 | 80 | \( \frac{1}{3} \) | 26.67 |
| \( \{A\} \) | 100 | 220 | 120 | \( \frac{1}{6} \) | 20.00 |
| \( \{C\} \) | 60 | 140 | 80 | \( \frac{1}{6} \) | 13.33 |
| \( \{A, C\} \) | 180 | 300 | 120 | \( \frac{1}{3} \) | 40.00 |
\( 26.67 + 20.00 + 13.33 + 40.00 = 100.00 \)
プレイヤー \( C \) に関する計算- 寄与度: \( v(S \cup \{A\}) - v(S) \)
- 重み: \( \frac{|S|!(|N| - |S| - 1)!}{|N|!} \)
| 部分集合 \( S \) | \( v(S) \) | \( v(S \cup \{C\}) \) | 寄与度 | 重み | 寄与度 × 重み |
|---|---|---|---|---|---|
| \( \{\} \) | 0 | 60 | 60 | \( \frac{1}{3} \) | 20.00 |
| \( \{A\} \) | 100 | 180 | 80 | \( \frac{1}{6} \) | 13.33 |
| \( \{B\} \) | 80 | 140 | 60 | \( \frac{1}{6} \) | 10.00 |
| \( \{A, B\} \) | 220 | 300 | 80 | \( \frac{1}{3} \) | 26.67 |
\( 20.00 + 13.33 + 10.00 + 26.67 = 70.00 \)
重みの計算ステップ(例:プレイヤーCの2行目)
部分集合 \( S \) のメンバー数 \( |S| \) を計算します。2行目の場合、\( S = \{B\} \) なので、 \( |S| = 1 \) となります。 \( N \) の値は \( \{A, B, C\} \) のメンバー数である \( 3 \) です。ここで、重みの計算は \( \frac{1! \cdot (3 - 1 - 1)!}{3!} \) となります。階乗の計算は、\( 1! = 1 \)、\( 1! = 1 \)、および \( 3! = 3 \times 2 \times 1 = 6 \) となります。したがって、重みは \( \frac{1 \cdot 1}{6} = \frac{1}{6} \) となります。
結果
| プレイヤー | Shapley Value |
|---|---|
| \( A \) | 130.00 |
| \( B \) | 100.00 |
| \( C \) | 70.00 |
違った視点の計算方法
A,B,Cの全パターン並び(6通り)で各プレイヤーが参加した際に、どれだけ点数が増加するかを算出し、平均をとることで算出できます。
| 順番 | A | B | C |
|---|---|---|---|
| \( A \rightarrow B \rightarrow C \) | 100 | 120 | 80 |
| \( A \rightarrow C \rightarrow B \) | 100 | 120 | 80 |
| \( B \rightarrow A \rightarrow C \) | 140 | 80 | 80 |
| \( B \rightarrow C \rightarrow A \) | 160 | 80 | 60 |
| \( C \rightarrow A \rightarrow B \) | 120 | 120 | 60 |
| \( C \rightarrow B \rightarrow A \) | 160 | 80 | 60 |
最後にプレイヤーごとに平均した得点を算出してShapley Valueになります。
結果:AのShapley Valueは130、BのShapley Valueは100、CのShapley Valueは70
関連用語の補足
- 協力ゲーム理論: 協力ゲーム理論は、複数のプレイヤー(特徴)が協力して成果を共有する際に、その貢献を公平に分配する理論です。 SHAPやその他の説明可能なAI手法では、この理論を基にして各特徴の寄与を計算します。
キーワードまとめ
XAI (eXplainable AI)、CAM (Class Activation Map)、Grad-CAM、局所的な解釈、大域的な解釈、LIME、SHAP、Shapley Value、協力ゲーム理論